I've been hearing a lot of discussion about riding to/from Whistle Bend, plus perception of traffic problems with getting from Whistle Bend. So, I put some thought on what might be the best way to get there if we wanted to invest in active transportation infrastructure so people can get between downtown and Whistle Bend safely and comfortably by bike, or better yet, by e-bike!
I don't live in Whistle Bend, nor do I bike there often, so I really don't know much. But hey, lack of knowledge has never stopped people from expressing their opinion on the Internet! So here we go...
Routes:
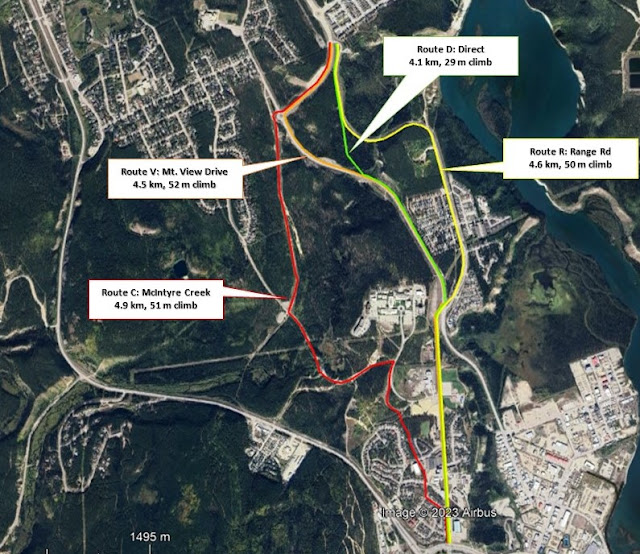
I looked at four routes to/from Whistle Bend to a common point to downtown. To make a fair comparison, I chose the top of 2-Mile Hill (as opposed to going down Mt.View Drive/Copper Rd., you will see why). The image below shows the routes, plus the distance and total climb if riding south from Whistle Bend to 2-Mile Hill. These routes are:
- Route C: McIntyre Creek - assume a protected path up Whistle Bend Way to the roundabout, then a paved multi-use path connecting along the powerline/waterline to the Porter Creek trail crossing McIntyre Creek. I assumed the path would be optimized south of there to avoid the gratuitous hill to Takhini, instead following the natural, less hilly route along University Drive to Takhini.
- Route M: Mountain View Drive - similar to Route C, assume a protected path up Whistle Bend Way to the roundabout, then a separated, protected path along east side Mountain View all the way to Range Rd.* From there, following the protected cycleway along Range Rd to 2 Mile Hill.
- Route D: Direct Route - this is the creative route: build a direct, paved, lit, multi-use path linking Range Road at Whistle Bend to Mountain View Drive, thereby avoiding the hill with a nice gentle downhill through the forest! Then follow a separated, protected path along east side Mountain View all the way to Range Rd.* From there, following the protected cycleway along Range Rd to 2 Mile Hill.
- Route R: Range Road - assume a protected path built along the west side of Range Road, all the way to its crossing of Mountain View Drive*. From there, following the protected cycleway along Range Rd to 2 Mile Hill.
Results:
What do we see? Well, my so-called "Direct Route" is shortest by almost half a kilometer, but most importantly, it has over 40% less climb. That is a lot! 29 m of climb vs. about 50m of climb for all the other three options.
- Route C: McIntyre Creek - 4.9 km - 51 m climb
- Route V: Mountain View Drive - 4.5 km - 52 m climb
- Route D: Direct - 4.1 km - 29 m climb
- Route R: Range Rd. - 4.6 km - 50 m climb
Below are climb profiles of the four routes, starting at Whistle Bend and finishing at 2 Mile Hill. Note the vertical scale is not the same in all of these:
 |
| Route V: Mountain View Drive elevation profile |
 |
| Route C: McIntyre Creek route elevation profile |
 |
| Route D: Direct route elevation profile |
 |
| Route R: Range Road elevation profile |
*
* Here is a bonus idea: the north side of the Range Road and Mountain View Drive intersection is a natural place for an active transportation underpass. The reason is the topography is naturally suited for creating the separation. Thus you could ride north from Takhini to Range Point or Whistle Bend, or even Porter Creek without having to cross Mountain View Drive! Even north-bound bus users would benefit because they could access the University without having to cross and stop busy traffic on Mountain View.
The other cool thing I learned recently is underpasses are better than overpasses for cycling because you carry your momentum, thus getting you half way up the other side without effort. Physics!